Dr. Dmitri Kopeliovich

• Hydrodynamic Force
• Hydrodynamic Bearing
• Reynolds Equation
• Practical Applications of Reynolds Equation
• Summary

A body moving through a liquid experiences a resistance generated by the hydrodynamic force. Effect of hydrodynamic forces is principal for reliable and stable work of hydrodynamic bearings. Action of hydrodynamic force upon a subject moving in a fluid may be shown by example of a water skier (Fig.1). The force Ft pulls the skier horizontally. The gravity force Fg acts vertically and is directed downwards. Reaction of water on the moving ski produces the hydrodynamic force, which can be presented as a combination of the horizontal vector Fd (drug force) and vertical vector Fl (lift force). When the skier is skimming on the water surface, the forces are balanced: Fd counteracts Ft in the horizontal direction, whereas Fl counteracts Fg in the vertical direction.



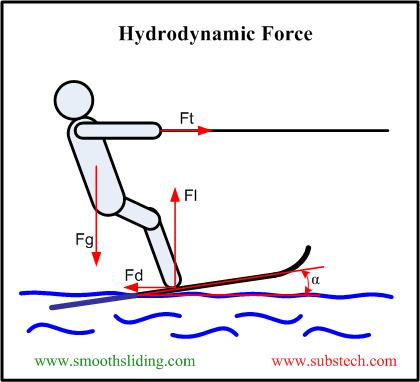
Fig.1 Hydrodynamic Force

The Fd-to-Fl ratio and their absolute values are determined by the skier speed, his weight and the wedge angle α (angle of attack). Too low towing speed and too little wedge α produce the lift force that is incapable to balance the gravity force and cause the skier to sink.

Thus for steady skiing, the three conditions are crucial:

• Sufficient speed;
• Sufficient wedge;
• Sufficient amount (depth) of the liquid (water).

to top

The same three conditions determine a stable work of hydrodynamic bearings. Fig.2 depicts a hydrodynamic bearing and a journal rotating in a clockwise direction. Hydrodynamic bearing is a bearing operating with hydrodynamic lubrication, in which the bearing surface is separated from the journal surface by the lubricant film generated by the journal rotation.



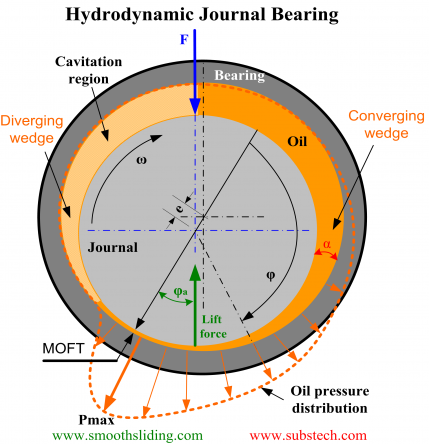
Fig.2 Hydrodynamic Bearing

Journal rotation causes pumping of the fluid flowing around the bearing in the direction of rotation.
The external force F displaces the journal from the bearing center. The journal surface is getting closer to the bearing surface forming a converging gap (wedge) α between the bearing and the journal surfaces. The presence of this oil wedge is indispensable to the normal operation of a hydrodynamic bearing.
The oil pressure creates a Lift Force separating the journal from the bearing surface. The Lift force counteracts the external force F. The lubricant enforced to squeeze through the gap between the bearing and journal surfaces produces the hydrodynamic friction.
The balance between the forces determines the final position of the journal: the value of minimum oil film thickness (MOFT) and the distance between the bearing and journal centers (eccentricity e). In the hydrodynamic regime, the journal “climbs” in the rotation direction at the angle φa (attitude angle).

to top

A theoretical analysis of hydrodynamic lubrication was carried out by Osborne Reynolds. Lubricant pressure distribution as a function of journal speed, bearing geometry, oil clearance and lubricant viscosity is described by the Reynolds equation that is a basis for designing hydrodynamic bearings:


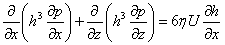
Where:
h – local oil film thickness,
η – dynamic viscosity of oil,
p – local oil film pressure,
U – linear velocity of journal,
x - circumferential direction,
z - longitudinal direction.

Close form solution of the Reynolds equation can not be obtained therefore finite elements method is used to solve it.

Analytical solutions of Reynolds equation exist only for certain assumptions:

• Sommerfeld Solution
  

The equation is solved with the assumption that there is no lubricant flow in the axial direction (infinitely long bearing assumption).

• Ocvirk Solution

Ocvirk solution for infinitely short bearing assumption neglects circumferential pressure gradients (first term of Reynolds equation).



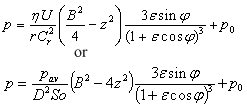
Where:
Cr – radial clearance Cr = (D-Dj)/2,
r – bearing radius,
Dj - journal diameter,
ε - eccentricity ratio ε = e/Cr,
e - absolute bearing eccentricity,
B – bearing length,
p0 - cavitation pressure,
So - Sommerfeld number So = F Ψ²/(DBωη),
F – bearing load,
Ψ – relative bearing clearance Ψ = (D-Dj)/D,
D – bearing diameter,
η – dynamic viscosity of oil,
ω – angular speed of journal.

to top

The Reynolds equation is used for calculating hydrodynamic conditions of bearing operation: minimum oil film thickness, oil temperature rise, coefficient of friction, power friction loss, oil flow rate. When a bearing is being designed, theoretical simulation of hydrodynamic lubrication is performed to optimize the bearing dimensions and lubrication conditions.

Here are three examples of application of the Reynolds Equation for optimization of hydrodynamic bearing conditions.

Table 1 Input Parameters

Some of the calculation results are presented in Fig.3-6.

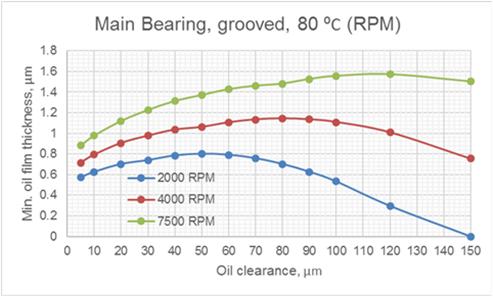
Fig.3 Effect of Oil Clearance and Rotation Speed on MOFT

The most stable hydrodynamic regime of lubrication is established at the maximum value of minimum oil film thickness (MOFT). According to the graphs in Fig.3, the optimal values of oil clearance for the bearing are as follows:
At 2000 RPM – 50 µm;
At 4000 RPM – 80 µm;
At 7500 RPM – 120 µm.

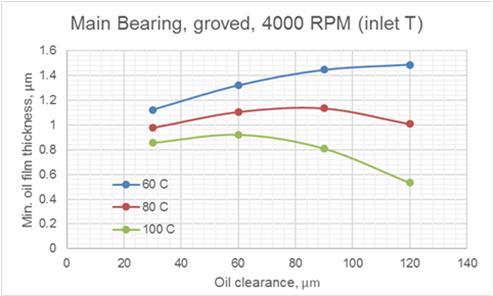
Fig.4 Effect of Oil Clearance and Oil Inlet Temperature on MOFT



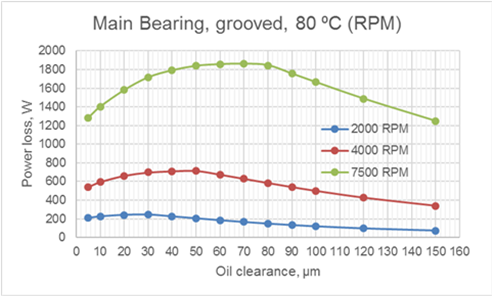
Fig.5 Effect of Oil Clearance and Rotation Speed on Power Loss



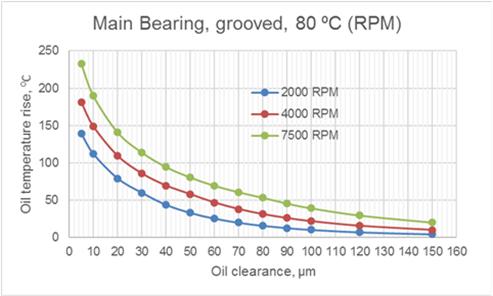
Fig.6 Effect of Oil Clearance and Rotation Speed on Oil Temperature Rise

Table 2 Input Parameters

The results of calculations are depicted in Fig.7, 8 Low rotation speeds (100-200 RPM) result in reduction of the values of minimum oil film thickness to the critical level below 0.5 µm (Fig.7).

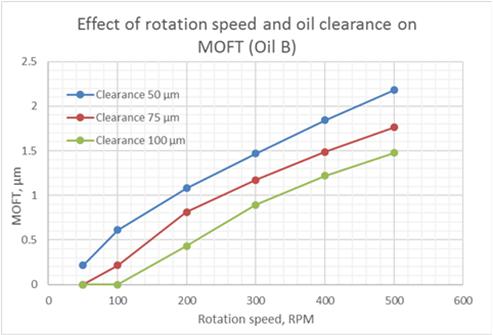
Fig.7 Effect of Rotation Speed and Oil Clearance on MOFT



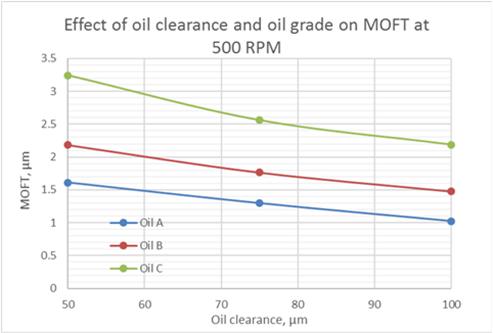
Fig.8 Effect of Oil Clearance and Oil Grade on MOFT

Table 3 Input Parameters

The calculations are made for two oil grades having different viscosity. The grade E is more viscous than the Grade D. The results of calculations are depicted in Fig.9-11.



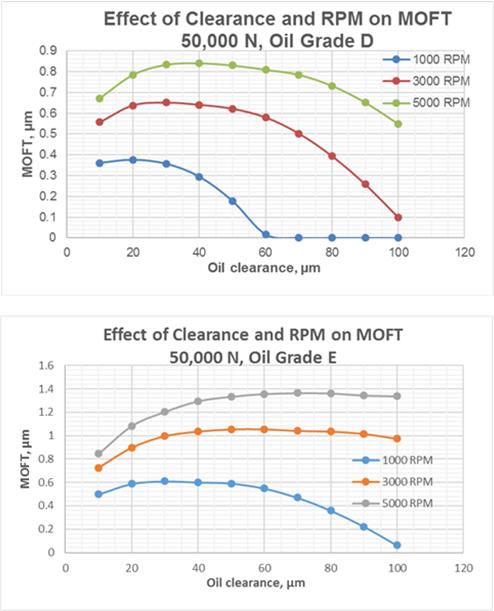
Fig.9 Effect of Rotation Speed and Oil Clearance on MOFT for Oil Grades D and E

The graphs in Fig.9 show that the oil grade E produces more stable hydrodynamic lubrication in wide ranges of the oil clearance and rotation speeds. However, the energy losses in hydrodynamic friction with the oil grade E are greater by approx. 60 % than those with the oil grade E (Fig.10).



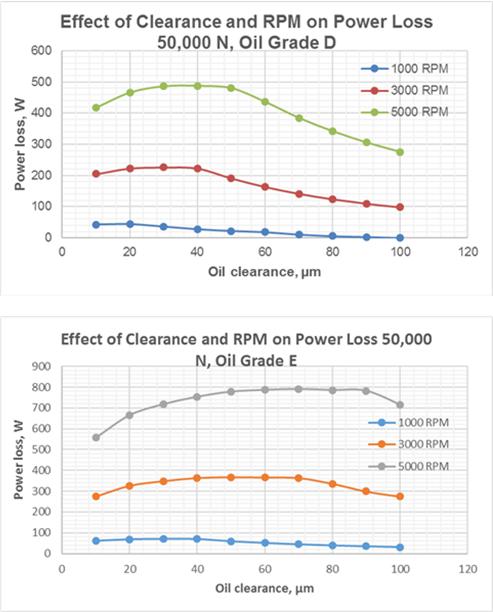
Fig.10 Effect of Rotation Speed and Oil Clearance on Power Loss for Oil Grades D and E




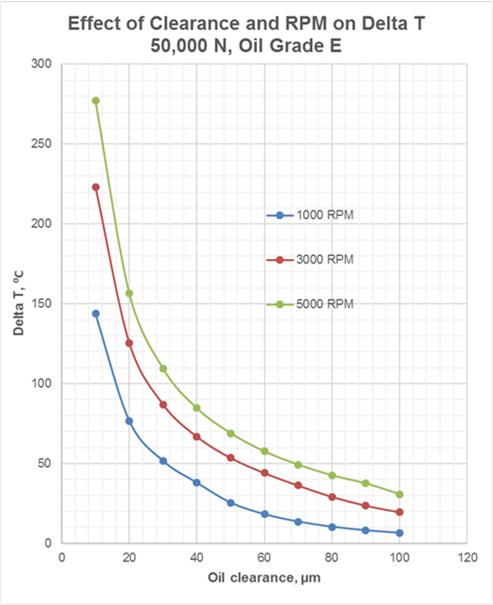
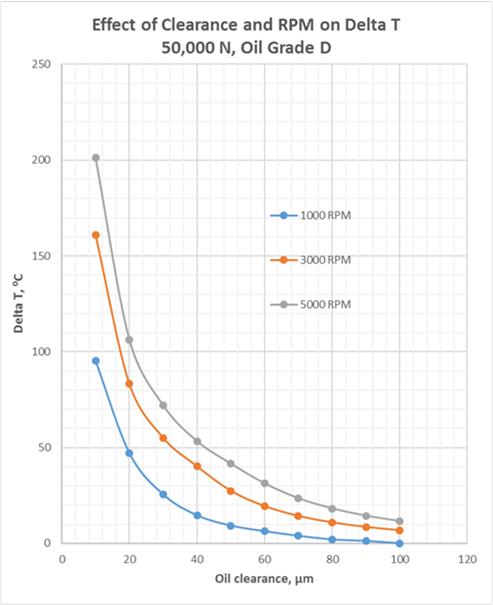
Fig.11 Effect of Rotation Speed and Oil Clearance on Oil Temperature Rise for Oil Grades D and E

Fig.12 depict the effect of the bearing loading on stability of hydrodynamic lubrication within a range of oil clearance value.



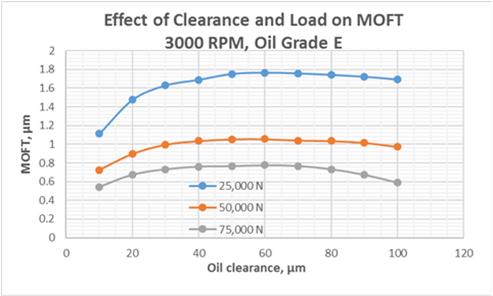
Fig.12 Effect of Oil Clearance and Bearing Load on MOFT

to top

• Basics of hydrodynamic force are explained by the example of a water skier.

• Work of hydrodynamic bearing, conditions and principal parameters of hydrodynamic lubrication are considered.

• Theoretical foundation of hydrodynamic bearing (Reynolds Equation) is described.

• Practical examples are given on application of Reynolds equation for calculating hydrodynamic conditions of bearing operation: minimum oil film thickness, oil temperature rise, power friction loss.

• It is shown, how theoretical simulations of hydrodynamic lubrication help to optimize the bearing design and lubrication conditions.

to top

• Bearings in internal combustion engines
• Engine parameters determining bearing loading
• Lubrication regimes
• Hydrodynamic journal bearing
• Hydrodynamic lubrication theory
• Geometrical parameters of engine bearings
• Mechanisms of wear
• Requirements to engine bearing materials
• Engine bearing fatigue test
• Engine bearing materials
• Copper based bearing materials
• Manufacturing bi-metal strips for copper bearings
• Aluminum based bearing materials
• Continuous casting of aluminum based bearing alloys
• Manufacturing bi-metal strips for aluminum bearings
• Lead based engine bearing overlays
• Tin based engine bearing overlays
• Sputter bearing overlays
• Polymer based engine bearing overlays
• Engine bearing failure
• Selection of engine bearing materials
• Effect of low viscosity oils on engine bearings
• pMax Black™ - Strengthened Tri-metal Bearing Materials for High Performance Bearings
• U-Groove™ Modified Design of Oil Groove for High Performance Bearings
• ElliptiX™ Oil Hole of New Design for High Performance Bearings
• EccentriX™ Optimal Eccentricity for High Performance Bearings
• RadiaLock™ - Design of Crush Height for Reliable Press Fit of High Performance Bearings
• Optimization of Clearance Design for High Performance Engine Bearings
• Modern Trends In Materials For High Performance Engine Bearings
• Camshaft Bearings
• Ecological Aspects Of Engine Bearings
• Consistency in Bearing Wall Thickness
• Soft Strength of Racing Bearings
• Effect of oil viscosity on hydrodynamic friction of engine bearings
• Bearing Materials For Race Engines
• Oil Clearance and Engine Bearings
• Polymer Coated Bearings
• Development of Performance Bearings for Race Engines of Modern Design
• Failures of Engine Bearings and their Prevention
• Engine Bearing Housing and How it Affects Engine Bearings
• Polymer Coatings for Race Engine Bearings
• Heavy Duty Engine Bearings - Materials, Geometry, Failures
• Geometry of Engine Bearings
• Crush Height of Engine Bearings
• Materials for Engine Bearings

to Metals
to Engine bearings